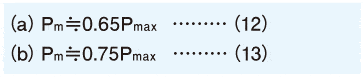Vida de un Sistema Lineal
Cuando un sistema lineal se reciproca bajo carga, un estrés continuo actúa sobre él, causando finalmente desprendimiento de su superficie del canal debido a fatiga del material. La distancia que un sistema lineal viaja antes de que su desprendimiento ocurra es definido como la vida del sistema lineal. Un sistema lineal también se puede tornar inoperable debido a concreción, rotura, picaduras u oxidación. Sin embargo, estas causas se diferencian del desprendimiento ya que están relacionadas a la precisión de la instalación, ambiente de operación y método de relubricación.
Vida Nominal
Aún cuando un grupo de sistemas lineales del mismo lote de producción operen bajo condiciones idénticas, el tiempo de vida puede diferir debido a diferencias en las características de falla de fatiga del material. Este hecho evita la determinación del tiempo de vida exacto de uso de un sistema lineal en particular. Por lo tanto, la vida nominal es definida estadísticamente como la distancia del 90% del viaje del sistema lineal antes de que se dé el desprendimiento.
Clasificación de Carga Dinámica Básica (de acuerdo con el ISO14728-1＊2) y Clasificación de Rotación Dinámica Básica
La vida de un sistema lineal es expresado en términos de la distancia viajada. Por lo tanto, la vida de un sistema lineal es calculada de forma opuesta utilizando la carga admisible que logra cierta distancia de viaje. Esta carga admisible es llamada clasificación de carga dinámica básica. La clasificación de carga dinámica básica es definida como una carga constante en peso y dirección que puede lograr una distancia de viaje de 50×103m en el sistema lineal. NB asume que la carga es aplicada desde la parte de arriba como una carga radial normal, ya que las clasificaciones de carga dinámica básica cambian dependiendo de la dirección aplicada de carga. Las clasificaciones de carga dinámica básica en las tablas dimensionales están basadas en este principio. Los ejes nervados pueden llevar carga de rotación, por lo que la clasificación de rotación dinámica básica es definida para el Eje Nervado.＊2: Esto no aplica para algunos productos.
Estimación de Vida Nominal
La estimación de la vida nominal depende del tipo de elemento rodante. Las ecuaciones (3) y (4) son utilizadas para el elemento de bola y para el elemento rodillo, respectivamente. La ecuación (5) es utilizada cuando hay carga de rotación presente.
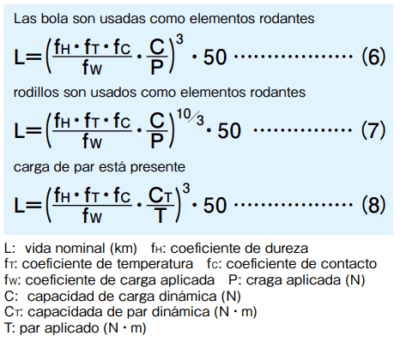
En la aplicación actual, numerosos factores variables están presentes, tales como la precisión del riel/eje de guía, condiciones de montaje, condiciones de operación, vibración e impacto, etc. Por lo tanto, calcular la carga aplicada real de forma precisa es extremadamente complicado. En general, el cálculo es simplificado utilizando estos coeficientes representando estos factores: coeficiente de dureza (fH), coeficiente de temperatura (fT), coeficiente de contacto (fC), y coeficiente de carga aplicada (fW). Tomando en consideración estos coeficientes, las Ecuaciones (3) a la (5) se convierten en las Ecuaciones (6) a la (8).
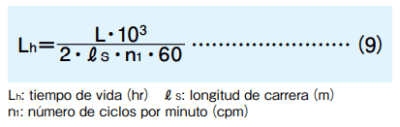
Cuando la distancia de viaje por unidad de tiempo es constante, la vida nominal puede ser expresada en términos de tiempo (hora). La ecuación (9) muestra la relación entre longitud de carrera, número de ciclos por minuto y el tiempo de vida.
Coeficiente de Dureza(ｆＨ)
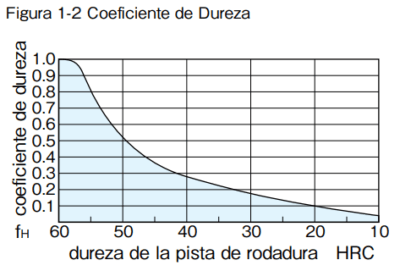
En el sistema lineal, el riel o eje guía funciona como un canal para los elementos rodantes. Por lo tanto, la dureza del riel o eje es un factor importante para determinar la carga nominal. La carga nominal disminuye conforme la dureza disminuye por debajo de 58HRC. Los productos NB mantienen una dureza apropiada empleando tecnología avanzada de tratamiento con calor. En caso de utilizar un riel o eje de dureza insuficiente, por favor incluye el coeficiente de dureza (la figura a la derecha) en la ecuación del cálculo de la vida.
Coeficiente de Temperatura(ｆＴ)
Para proveer a los productos NB de características de bajo desgaste, se les endurece mediante tratamiento con calor. Si la temperatura del sistema lineal excede 100℃, , la dureza es disminuida por el efecto de atemperado y conforme la carga nominal disminuye. La figura de la derecha muestra el coeficiente de temperatura conforme la dureza cambia con la temperatura.
Coeficiente de Contacto(ｆＣ)
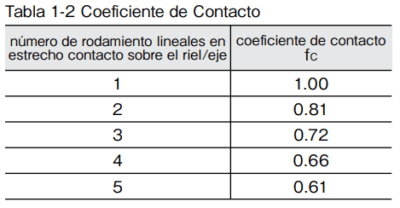
Cuando se usa más de un soporte en contacto cercano, el coeficiente de contacto de be ser tomado en consideración debido a la variación de los productos y la precisión de la superficie de montura. La tabla a la derecha muestra el coeficiente de contacto para el cálculo de la vida.
Coeficiente de Carga Aplicada(ｆＷ)
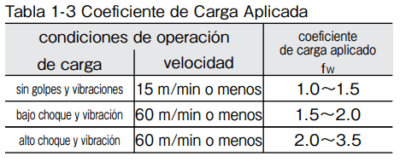
Cuando se calcula la carga aplicada, el peso de la masa, fuerza inercial, momento resultante del movimiento, y la variación con el tiempo deben ser estimados de forma precisa. Sin embargo, es muy difícil estimar de forma precisa la carga aplicada debido a la existencia de diversas variables, incluyendo las condiciones de inicio/fin del movimiento recíproco y del choque/vibración. La estimación es simplificada utilizando los valores proporcionados en la tabla.
Cálculo de la Carga Aplicada(1)
Las tablas abajo muestran las fórmulas para el cálculo de carga aplicada para aplicaciones típicas.
W: carga aplicada (N) P1 – P4: carga aplicada al sistema lineal (N) X,Y: alcance del sistema lineal (mm)
x, y, 
: distancia a la carga aplicada o al centro de gravedad funcional (mm) g: aceleración gravitacional (9.8 x 103mm/s2)
V: velocidad (mm/s) t1: tiempo de aceleración (seg) t3: tiempo de desaceleración (seg)
Bajo condiciones estáticas o movimiento de velocidad constante
|
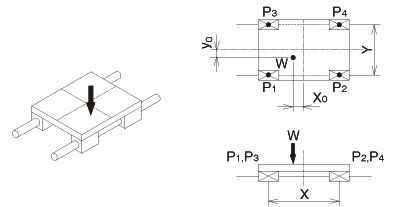
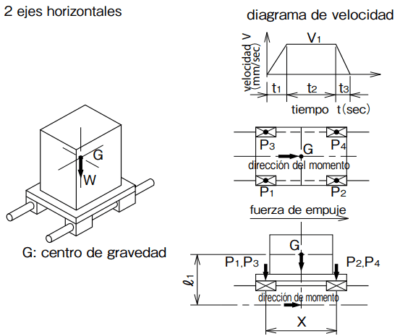
2 ejes horizontales
|
fórmula de cálculo de carga aplicada
|
 |
 |
|
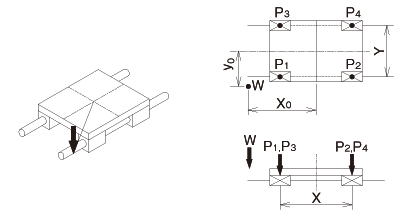
2 ejes horizontales, salientes
|
fórmula de cálculo de carga aplicada
|
 |
|
|
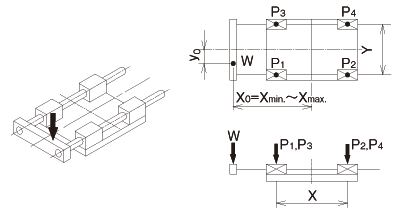
2 ejes horizontales, ejes en movimiento
|
fórmula de cálculo de carga aplicada
|
 |
|
|
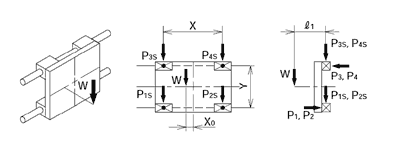
2 ejes horizontales, ejes laterales
|
fórmula de cálculo de carga aplicada
|
 |
 |
|
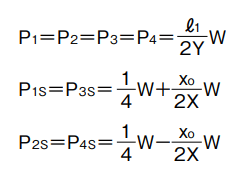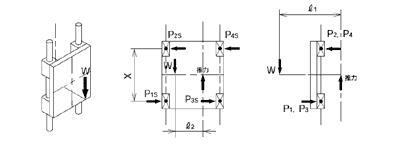
2 ejes verticales
|
fórmula de cálculo de carga aplicada
|
 |
 |
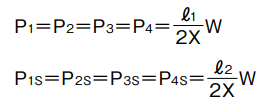Bajo condiciones de aceleración constante
|
2 ejes horizontales
|
fórmula de cálculo de carga aplicada
|
 |
 |
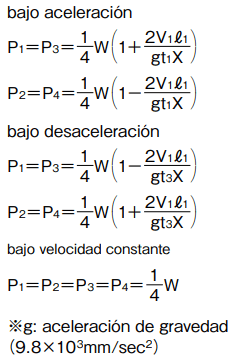Coeficiente Equivalente
Los sistemas lineales son generalmente utilizandos con dos ejes, cada uno con un par de soportes instalados. Sin embargo, debido a la limitación de espacio, debe haber una aplicación en la cual haya un eje con uno o dos soportes en contacto cercano instalados. En dicho caso, multiplique el momento aplicado por el coeficiente de momento equivalente mostrado en la tabla para el cálculo de carga aplicada. La siguiente es una fórmula para calcular la carga de momento equivalente cuando es aplicado un momento al sistema lineal.
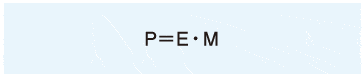
P: carga de momento equivalente por soporte(N)
E: coeficiente de momento equivalente
M: momento aplicado(N・mm)
Cálculo de la Carga Aplicada((2)
Las tablas de abajo muestran las fórmulas para determinar la carga aplicada cuando el momento es aplicado al sistema lineal.
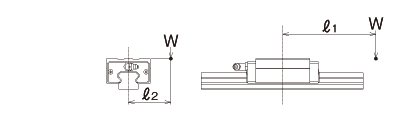
W: carga aplicada (N) P: carga aplicada al sistema lineal (N) : distancia a la carga aplicada o al centro de gravedad funcional (mm)
Aplicación de eje sencillo
|
1 eje horizontal, 1 bloque
|
fórmula de cálculo de carga aplicada
|
 |
 |
|
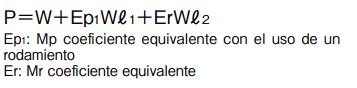1 eje lateral,1 bloque
|
fórmula de cálculo de carga aplicada
|
 |
 |
|
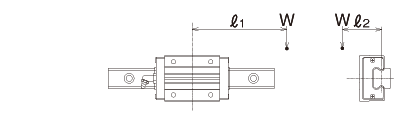1 eje vertical, 1 bloque
|
afórmula de cálculo de carga aplicada
|
 |
 |
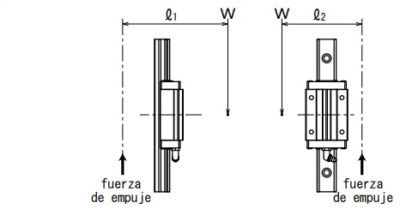aplicación de 2 ejes
|
2 ejes horizontales, 1 bloque para cada uno
|
fórmula de cálculo de carga aplicada
|
 |
 |
|
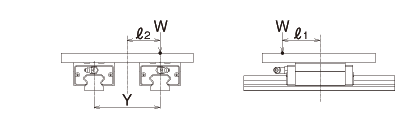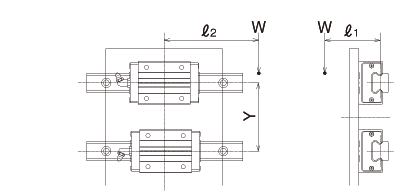
2 ejes laterales, 1 bloque cada uno
|
fórmula de cálculo de carga aplicada
|
 |
 |
|
2 ejes verticales, 1 bloque cada uno
|
fórmula de cálculo de carga aplicada
|
 |
 |
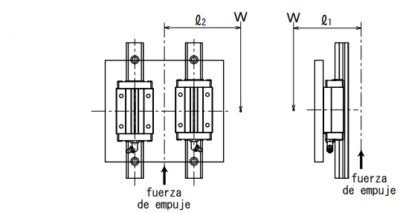Carga Aplicada Promedio
La carga aplicada al sistema lineal generalmente varía con la distancia de viaje dependiendo de cómo sea operado el sistema. Esto incluye los procesos de inicio/fin del movimiento recíproco y trabajo en el sistema. La carga aplicada promedio es utilizada para computar la vida correspondiente a las condiciones reales de la aplicación.
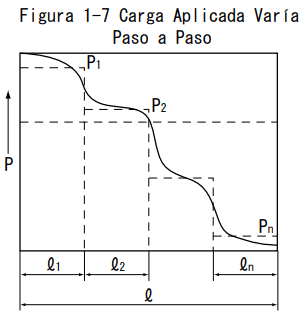
Cuando la carga varía en forma escalonada con la distancia de viaje
1 es la distancia de viaje bajo carga2 es la distancia de viaje bajo carga
n es la distancia de viaje bajo la carga Pn
La carga aplicada promedio Pm es obtenida mediante la siguiente ecuación.
Pm: carga promedio aplicada (N): distancia de viaje total (m)
Cuando la carga aplicada varía en forma lineal con la distancia de viaje
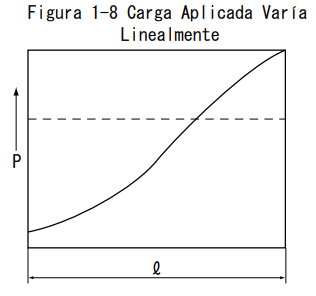
La carga promedio aplicada Pm es una p aproximada por la siguiente ecuación.
Pmin: carga aplicada mínima (N)
Pmax: carga aplicada máxima (N)
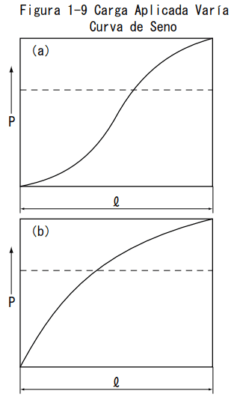
Cuando la carga aplicada dibuja una curva sinusoide como se muestra en la figura de la derecha (a) y (b)
La carga promedio aplicada Pm es aproximada por las siguientes ecuaciones.
